
Multiply coefficients in front of radical signs, if any.Ģ.

Multiplying square roots with coefficientsġ.

Take out the square root of the perfect square. In this example, simplify √49 to 7 and place it in front of the remaining expression, √2. In this case, you can simplify √98 to √2 and √49 - a perfect square.ģ. Simplify the radicand by factoring out all perfect squares. If there are no perfect squares in the radicand, it’s already simplified. Multiply each radicand the same way you would without the radical, or square root symbol.Ģ. One thing’s for sure - people in those professions learned math in school as kids and they’re still using it today! Part Two: 3 Simple methods for multiplying square roots Multiplying square roots without coefficientsġ. There are more, too! While some will have to calculate equations every day, others will use the concepts to make estimates. Knowing the square footage of their future homes.For example, multiplying square roots can be important for: ☝️Īnd you should be prepared to provide them with legitimate answers. No matter how well you teach these algebraic concepts, students will always ask that question. When will I ever need to multiply square roots? However, root indexes are necessary when calculating higher indexed roots like cube, fourth, or fifth roots. Many questions about finding square roots don’t include the root index. Students seeing this for the first time will likely have some questions: What’s that check mark-looking symbol? Why’s there a tiny number over it?īrett Berry, the founder of Math Hacks, created a clear and concise image with all the root terminology in her article on understanding logarithms and roots. In math class, this kind of equation would look like: In the visual below we see the square root of 16 is 4 because 4 squared, or 42, is 16. That said, perfect square numbers are the most effective ones to use when teaching students about multiplying square roots. Like you saw above, square roots undo squaring, so it’s impossible for negative numbers to have square roots. This is because any number times itself is positive, or zero - you can never get a negative product when you square a negative number. It’s only possible to take the square root of non-negative numbers - even ones that don’t yield whole numbers.
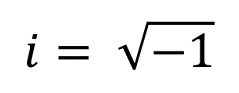
Put another way, finding the square root is the opposite process of squaring a number. The square root of a number refers to the factor you can multiply by itself to get that number.
#NEGATIVE SQUARE ROOT HOW TO#
Learning how to multiply square roots is one cobblestone on the scenic road to understanding algebra’s real-life relevance.Įducators like yourself know it’s not always easy to make these abstract and complex concepts engaging and fun. Just because you don’t see Xs and Ys doesn’t mean you aren’t using algebra every day. You want them to realize what French mathematician, Jean de Rond d’Alembert, famously said: “algebra is generous she often gives more than is asked of her.” But, you fear they might be thinking: “In math class, we learned more about algebra, such as X + 10 = Y, but why should I care?” Your students know how to multiply exponents, but now it’s time to teach them about multiplying square roots and the wonderful world of pre-algebra.


 0 kommentar(er)
0 kommentar(er)
